Multistate Modeling with a time-to event mediator Mediator
2022-03-30
Source:vignettes/multistate_model.Rmd
multistate_model.RmdThis example demonstrates how to use cmest when there is a time-to-event mediator. For this purpose, we simulate several situation: 1) one baseline confounder. 2) multiple baseline confounders.
Data contains a binary exposure \(A\), a time-to-event mediator \(M\), a time-to-event outcome \(Y\) and multiple types of confounders \(C^{'}\).
We can define the Total Effect (TE) with respect to the survival function. \[TE=P(S>s|A=1,C) - P(S>s|A=0,C)\] The probability of surviving after time \(s\) between \(A=1\) and \(A=0\) patients had the distribution of time to mediator \(g\) been the same across the two exposure groups is referred as \("Residual\ Disparity" (RD)\) \[RD=P(S_g>s|A=1,C) - P(S_g>s|A=0,C)\] The probability of surviving after time \(s\) for subjects in exposure group \(A=a\) for a change in the time to mediator level is referred as \("Shifting\ Distribution\ Effect" (SD)\) \[SDE=P(S_g>s|A=1,C) - P(S_{g^*}>s|A=1,C)\]
There are three transitions: \(A\) \(\rightarrow\) \(M\), \(A\) \(\rightarrow\) \(Y\) and \(M\) \(\rightarrow\) \(Y\). So we define \(\alpha_{01}(t|A,C)\), \(\alpha_{02}(t|A,C)\) and \(\alpha_{12}(t|A,C)\) as the instantaneous hazard of three transitions respectively. \(\Lambda_{01}(s|A,C)\), \(\Lambda_{02}(s|A,C)\) and \(\Lambda_{12}(s|A,C)\) are the corresponding cumulative transition intensity functions.
We specify a semi-parametric proportional intensity model for the hazard of transitions: \[\alpha_{01}(t|A,C)=\alpha_{01}^{0}(t)e^{\beta_1A+\beta_2^{'}C}\]
\[\alpha_{02}(t|A,C)=\alpha_{02}^{0}(t)e^{\gamma_1A+\gamma_2^{'}C}\]
\[\alpha_{12}(t|t^{'},A,C)=\alpha_{12}^{0}(t)e^{\delta_1A+\delta_2t^{'}+\delta_3A*t^{'}+\delta_4^{'}C}\]
## Loading required package: dplyr##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union## Loading required package: mstate## Loading required package: survival## Loading required package: tidyrThe DAG for this scientific setting is:
cmdag(outcome = "Y", exposure = "A", mediator = "M",
basec = c("C1", "C2"), postc = NULL, node = TRUE, text_col = "white")
In this setting, we can use the multistate approach for stochastic interventions on a time-to event mediator in the presence of semi-competing risks. The results are shown below:
The multistate approach for stochastic interventions on a time-to event mediator in the presence of semi-competing risks
Binary exposure with multiple baseline confounders
This example demonstrates how to use cmest when there are one binary exposure, categorical baseline confounder C1 and continuous basline confounder C2. For this purpose, we simulate some data containing a categorical baseline confounder \(C_1\), a continuous basline confounder \(C_2\),a binary exposure \(A\), a time-to-event \(M\) and a time-to-event outcome \(Y\). The semi-parametric proportional intensity model for the hazard of 3 transitions are:
\[\alpha_{01}(t|A,C)=\alpha_{01}^{0}(t)e^{\beta_1A+\beta_2^{'}C} = \alpha_{01}^{0}(t)e^{-0.3*A+0.4*C_1+0.5*C_2}, where\ \alpha_{01}^{0}(t) = \lambda_{01}\gamma_{01}t^{\gamma_{01}-1} = 0.1*0.8*t^{0.8-1}\]
\[\alpha_{02}(t|A,C)=\alpha_{02}^{0}(t)e^{\gamma_1A+\gamma_2^{'}C} = \alpha_{02}^{0}(t)e^{0.2*A+0.3*C_1+0.4*C_2}, where\ \alpha_{02}^{0}(t) = \lambda_{02}\gamma_{02}t^{\gamma_{02}-1} = 0.07*0.12*t^{0.12-1}\]
\[\alpha_{12}(t|t^{'},A,C)=\alpha_{12}^{0}(t)e^{\delta_1A+\delta_2t^{'}+\delta_3A*t^{'}+\delta_4^{'}C} = \alpha_{12}^{0}(t)e^{0.*4A+0*t^{'}+(-0.2)*A*t^{'}+0.5*C_1+0.6*C_2}, where\ \alpha_{12}^{0}(t) = \lambda_{12}\gamma_{12}t^{\gamma_{12}-1} = 0.1*0.5*t^{0.5-1}\]
#generate dataset
set.seed(1)
#build a function to generate time-to-event data
gen_srv <- function(n, lambda, gamma, beta, X){
X = as.matrix(X)
beta = as.matrix(beta, ncol=1)
T = (-log(runif(n)) / (lambda * exp(X %*% beta)))^(1/gamma) #weibull distribution
return(T)
}
n <- 5000
A = sample(c(0,1),replace=TRUE, size=n, c(0.7,0.3)) #binary exposure
c1 = sample(c(0,1),replace=TRUE, size=n,c(0.6, 0.4)) #binary confounder
c2 = rnorm(n, mean = 1, sd = 1) #continuous confounder
id=c(1:n)
full = data.frame(id,A,c1,c2)
M = gen_srv(n=n, lambda = 0.1,gamma = 0.8, beta = c(-0.3,0.4,0.5), X=data.frame(A,c1,c2)) #time to event mediator
Y = gen_srv(n=n, lambda = 0.07, gamma = 0.12, beta = c(0.2,0.3,0.4), X=data.frame(A,c1,c2)) #time to event outcome
data = data.frame(id = c(1:n), M = M, Y = Y)
# indicator for event
data$M_ind = ifelse(data$M <= data$Y, 1, 0)
data$Y_ind = 1
data <- merge(data,full , by = "id")
#modify Y distribution
trans_matrix = transMat(x = list(c(2, 3), c(3), c()), names = c("A", "M", "Y"))
covs = c("A","M", "c1","c2")
pre_data = msprep(time = c(NA, "M", "Y"), status = c(NA, "M_ind", "Y_ind"),
data = data, trans = trans_matrix, keep = covs)
pre_data = expand.covs(pre_data, covs, append = TRUE, longnames = FALSE)
pre_data$A_M.3 = pre_data$A.3*pre_data$M.3
# resample for T < S
data_23= pre_data[which(pre_data$trans == 3),]
data_23_tem = data.frame(id = rep(NA,dim(data_23)[1]),
new_y = rep(NA,dim(data_23)[1]))
for(i in 1:dim(data_23)[1]){
data_23_tem$id[i] = data_23$id[i]
repeat {
# do something
time_test = gen_srv(n = 1,
lambda = 0.1,
gamma = 0.5,
beta = c(as.numeric(0.4),
0,
as.numeric(0.5),
as.numeric(0.6),
as.numeric(-0.2)),
X = data_23[i, c("A.3", "M.3", "c1.3","c2.3", "A_M.3")])
# exit if the condition is met
if (time_test > data_23[i,"M.3"]) break
}
data_23_tem$new_y[i] = time_test
}
data_temp = merge(data, data_23_tem, by = "id", all = T)
#modify Y and M
data_temp$Y[which(data_temp$M_ind == 1)] = data_temp$new_y[which(data_temp$M_ind == 1)]
data_temp$M[which(data_temp$M_ind == 0)] = data_temp$Y[which(data_temp$M_ind == 0)]
data_final = data_temp
data_final$Y_day = data_final$Y*30
data_final$M_day = data_final$M*30
data_final$Y_ind[which(data_final$Y > 24)] = 0 #censored data
data_final$Y[which(data_final$Y> 24)] = 24
data_final$Y_day[which(data_final$sY_day > 24*30)] = 24*30
data_final$M_ind[which(data_final$M > 24)] = 0
data_final$M[which(data_final$M > 24)] = 24
data_final$M_day[which(data_final$M_day > 24*30)] = 24*30
data_final$A = as.factor(data_final$A) #generate a factor exposure
data = data_final %>% select(id,A,M,Y,M_ind,Y_ind,c1,c2)
surv_biE <- cmest(data = data, model = 'multistate',total_duration = 24, time_grid = 1,survival_time_fortable = 22, exposure = 'A',mediator = 'M', outcome = 'Y',
event = "Y_ind",mediator_event = "M_ind", basec = c('c1','c2'),
basecval = c('c1' = '0','c2' = '0'),astar = '0',a='1',nboot=100)
summary(surv_biE)## Causal Mediation Analysis
##
## # Multistate Model:
##
## [1] "coxph(Surv(Tstart, Tstop, status) ~ A.1 + A.2 + A.3 + c1.1 + c1.2 + c1.3 + c2.1 + c2.2 + c2.3 + A.3*M.3 + strata(trans))"
## # Multistage Model Estimation:
##
## Call:
## coxph(formula = formula, data = msdata, control = coxph.control(timefix = FALSE),
## model = TRUE, method = method)
##
## n= 13660, number of events= 6002
##
## coef exp(coef) se(coef) z Pr(>|z|)
## A.1 -0.239015 0.787403 0.036657 -6.520 7.01e-11 ***
## A.2 0.158376 1.171606 0.080433 1.969 0.048950 *
## A.3 0.524720 1.689986 0.076549 6.855 7.15e-12 ***
## c1.1 0.373070 1.452185 0.033836 11.026 < 2e-16 ***
## c1.2 0.292111 1.339251 0.076875 3.800 0.000145 ***
## c1.3 0.492009 1.635598 0.049994 9.841 < 2e-16 ***
## c2.1 0.497082 1.643918 0.017739 28.022 < 2e-16 ***
## c2.2 0.413895 1.512698 0.039296 10.533 < 2e-16 ***
## c2.3 0.583305 1.791951 0.028083 20.771 < 2e-16 ***
## M.3 0.010430 1.010485 0.008322 1.253 0.210070
## A.3:M.3 -0.196897 0.821276 0.020651 -9.535 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## A.1 0.7874 1.2700 0.7328 0.8461
## A.2 1.1716 0.8535 1.0007 1.3717
## A.3 1.6900 0.5917 1.4545 1.9635
## c1.1 1.4522 0.6886 1.3590 1.5518
## c1.2 1.3393 0.7467 1.1519 1.5570
## c1.3 1.6356 0.6114 1.4829 1.8040
## c2.1 1.6439 0.6083 1.5877 1.7021
## c2.2 1.5127 0.6611 1.4006 1.6338
## c2.3 1.7920 0.5581 1.6960 1.8933
## M.3 1.0105 0.9896 0.9941 1.0271
## A.3:M.3 0.8213 1.2176 0.7887 0.8552
##
## Concordance= 0.64 (se = 0.004 )
## Likelihood ratio test= 1644 on 11 df, p=<2e-16
## Wald test = 1586 on 11 df, p=<2e-16
## Score (logrank) test = 1592 on 11 df, p=<2e-16
##
## # Relevant variable values:
## $a
## [1] "1"
##
## $astar
## [1] "0"
##
## $ref_table
## A M c1 c2
## 1 0 1 0 0
##
## $basecval
## c1 c2
## "0" "0"
##
## #Number of event in the data
## $Frequencies
## to
## from Start Mediator Outcome no event total entering
## Start 0 3660 702 638 5000
## Mediator 0 0 1640 2020 3660
## Outcome 0 0 0 2342 2342
##
## $Proportions
## to
## from Start Mediator Outcome no event
## Start 0.0000000 0.7320000 0.1404000 0.1276000
## Mediator 0.0000000 0.0000000 0.4480874 0.5519126
## Outcome 0.0000000 0.0000000 0.0000000 1.0000000
##
## #Point Estimation for time point of interest
## TE RD SD
## 1 0.0305422 0.01137226 0.01916994
## #SE for Point Estimation for time point of interest
## se_te se_rd se_sd
## 1 8.998994e-05 8.349577e-05 2.700766e-05
## #CI for Point Estimation for time point of interest
## TE RD SD
## 0.011042447 -0.003312541 0.014686265
## TE RD SD
## 0.04991983 0.02803755 0.02522333
## #Point Estimation table for time point of interest
## TE RD SD
## Point estimate 0.0305 0.0114 0.0192
## 95% CI (0.011, 0.0499) (-0.0033, 0.028) (0.0147, 0.0252)
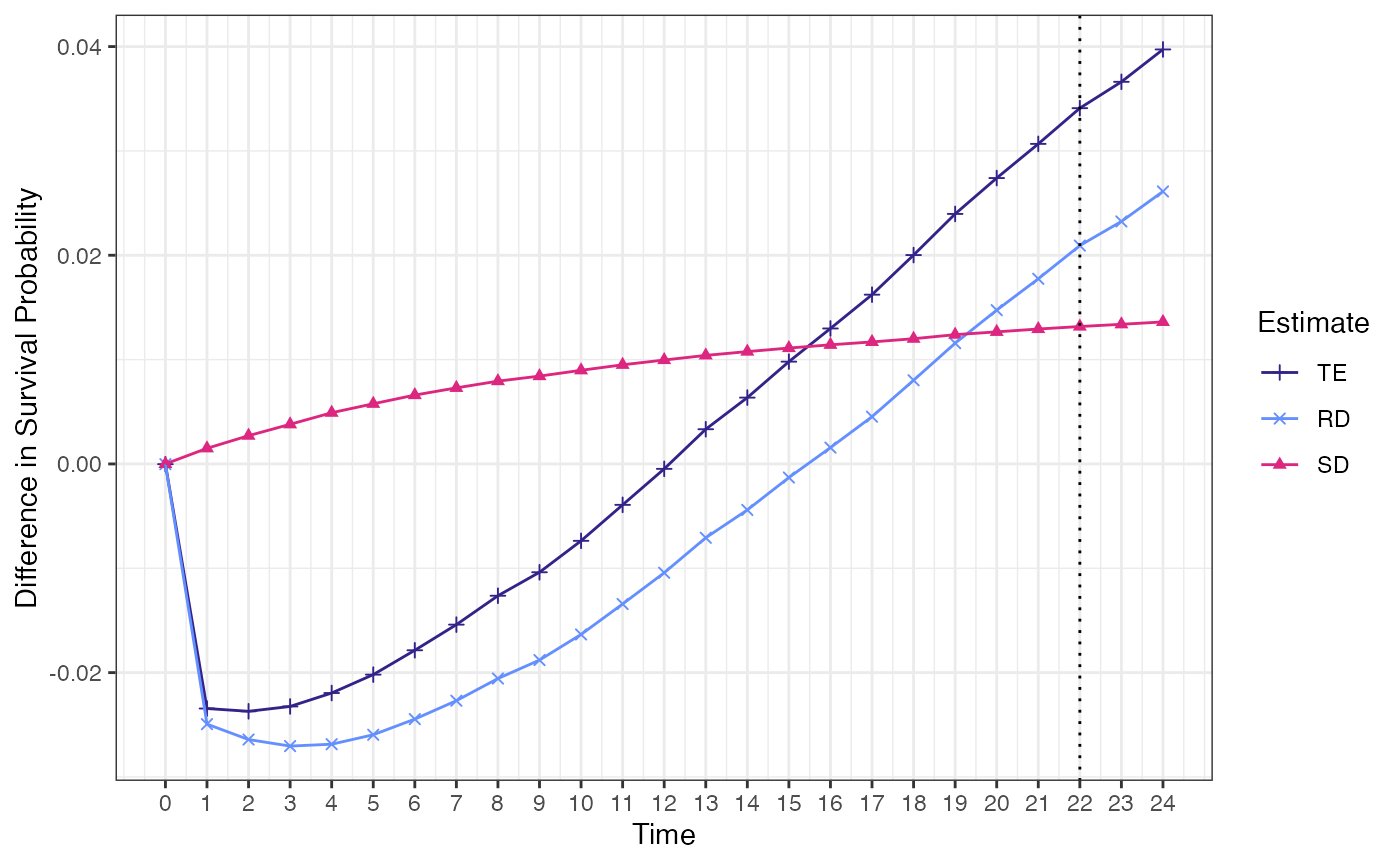
ggcmest(surv_biE)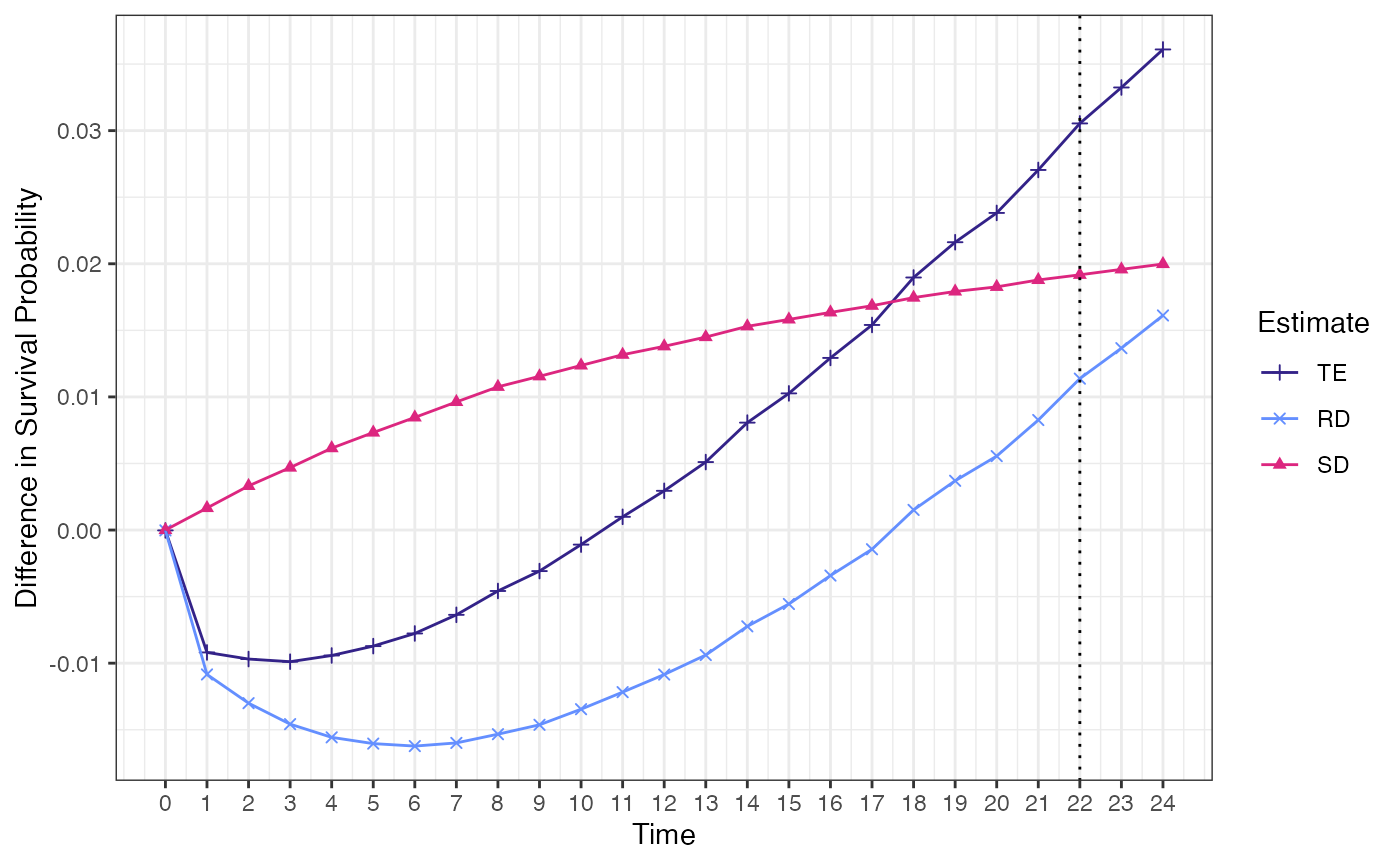
Categorical exposure with multiple baseline confounders
This example demonstrates how to use cmest when there are one categorical exposure, categorical baseline confounder C1 and continuous basline confounder C2. For this purpose, we simulate some data containing a categorical baseline confounder \(C_1\), a continuous basline confounder \(C_2\),a categorical exposure \(A\), a time-to-event \(M\) and a time-to-event outcome \(Y\). The semi-parametric proportional intensity model for the hazard of 3 transitions are:
\[\alpha_{01}(t|A,C)=\alpha_{01}^{0}(t)e^{\beta_1A+\beta_2^{'}C} = \alpha_{01}^{0}(t)e^{-0.3*A_1+(-0.2*A_2)+0.4*C_1+0.5*C_2}, where\ \alpha_{01}^{0}(t) = \lambda_{01}\gamma_{01}t^{\gamma_{01}-1} = 0.1*0.8*t^{0.8-1}\]
\[\alpha_{02}(t|A,C)=\alpha_{02}^{0}(t)e^{\gamma_1A+\gamma_2^{'}C} = \alpha_{02}^{0}(t)e^{0.2*A_1+0.3*A_2+0.3*C_1+0.4*C_2}, where\ \alpha_{02}^{0}(t) = \lambda_{02}\gamma_{02}t^{\gamma_{02}-1} = 0.07*0.12*t^{0.12-1}\]
\[\alpha_{12}(t|t^{'},A,C)=\alpha_{12}^{0}(t)e^{\delta_1A+\delta_2t^{'}+\delta_3A*t^{'}+\delta_4^{'}C} = \alpha_{12}^{0}(t)e^{0.4*A_1+0.3*A_2+0*t^{'}+(-0.2)*A_1*t^{'}+(-0.3)*A_2*t^{'}+0.5*C_1+0.6*C_2}, where\ \alpha_{12}^{0}(t) = \lambda_{12}\gamma_{12}t^{\gamma_{12}-1} = 0.1*0.5*t^{0.5-1}\]
#generate dataset
set.seed(1)
#build a function to generate time-to-event data
gen_srv <- function(n, lambda, gamma, beta, X){
X = as.matrix(X)
beta = as.matrix(beta, ncol=1)
T = (-log(runif(n)) / (lambda * exp(X %*% beta)))^(1/gamma) #weibull distribution
return(T)
}
n <- 10000
A = sample( c(0,1,2), size = n, replace=TRUE, prob=c(0.3,0.4,0.3))#categorical exposure
A=as.factor(A)
c1 = sample(c(0,1),replace=TRUE, size=n,c(0.6, 0.4)) #binary confounder
c2 = rnorm(n, mean = 1, sd = 1) #continuous confounder
id=c(1:n)
full = data.frame(id,A,c1,c2)
A1 = ifelse(full$A == 1, 1, 0)
A2 = ifelse(full$A == 2, 1, 0)
M = gen_srv(n=n, lambda = 0.1,gamma = 0.8, beta = c(-0.3,-0.2,0.4,0.5), X=data.frame(A1,A2,c1,c2)) #time to event mediator
Y = gen_srv(n=n, lambda = 0.07, gamma = 0.12, beta = c(0.2,0.3,0.4,0.5), X=data.frame(A1,A2,c1,c2)) #time to event outcome
data = data.frame(id = c(1:n), M = M, Y = Y)
# indicator for event
data$M_ind = ifelse(data$M <= data$Y, 1, 0)
data$Y_ind = 1
data <- merge(data,full , by = "id")
#modify Y distribution
trans_matrix = transMat(x = list(c(2, 3), c(3), c()), names = c("A", "M", "Y"))
covs = c("A","M", "c1","c2")
pre_data = msprep(time = c(NA, "M", "Y"), status = c(NA, "M_ind", "Y_ind"),
data = data, trans = trans_matrix, keep = covs)
pre_data = expand.covs(pre_data, covs, append = TRUE, longnames = FALSE)
pre_data$A1_M.3 = pre_data$A1.3*pre_data$M.3
pre_data$A2_M.3 = pre_data$A2.3*pre_data$M.3
# resample for T < S
data_23= pre_data[which(pre_data$trans == 3),]
data_23_tem = data.frame(id = rep(NA,dim(data_23)[1]),
new_y = rep(NA,dim(data_23)[1]))
for(i in 1:dim(data_23)[1]){
data_23_tem$id[i] = data_23$id[i]
repeat {
# do something
time_test = gen_srv(n = 1,
lambda = 0.1,
gamma = 0.5,
beta = c(as.numeric(0.4),
as.numeric(0.3),
0,
as.numeric(0.5),
as.numeric(0.6),
as.numeric(-0.2),
as.numeric(-0.3)),
X = data_23[i, c("A1.3","A2.3", "M.3", "c1.3","c2.3", "A1_M.3","A2_M.3")])
# exit if the condition is met
if (time_test > data_23[i,"M.3"]) break
}
data_23_tem$new_y[i] = time_test
}
data_temp = merge(data, data_23_tem, by = "id", all = T)
#modify Y and M
data_temp$Y[which(data_temp$M_ind == 1)] = data_temp$new_y[which(data_temp$M_ind == 1)]
data_temp$M[which(data_temp$M_ind == 0)] = data_temp$Y[which(data_temp$M_ind == 0)]
data_final = data_temp
data_final$Y_day = data_final$Y*30
data_final$M_day = data_final$M*30
data_final$Y_ind[which(data_final$Y > 24)] = 0 #censored data
data_final$Y[which(data_final$Y> 24)] = 24
data_final$Y_day[which(data_final$sY_day > 24*30)] = 24*30
data_final$M_ind[which(data_final$M > 24)] = 0
data_final$M[which(data_final$M > 24)] = 24
data_final$M_day[which(data_final$M_day > 24*30)] = 24*30
#data_final$A = as.factor(data_final$A) #generate a factor exposure
data_catE = data_final %>% select(id,A,M,Y,M_ind,Y_ind,c1,c2)
surv_catE <- cmest(data = data_catE, model = 'multistate',total_duration = 24, time_grid = 1,survival_time_fortable = 22, exposure = 'A',mediator = 'M', outcome = 'Y',
event = "Y_ind",mediator_event = "M_ind", basec = c('c1','c2'),
basecval = c('c1' = '0','c2' = '0'),astar = '0',a='2',nboot=100)
summary(surv_catE)## Causal Mediation Analysis
##
## # Multistate Model:
##
## [1] "coxph(Surv(Tstart, Tstop, status) ~ A1.1 + A1.2 + A1.3 + A2.1 + A2.2 + A2.3 + c1.1 + c1.2 + c1.3 + c2.1 + c2.2 + c2.3 + A1.3*M.3 + A2.3*M.3 + strata(trans))"
## # Multistage Model Estimation:
##
## Call:
## coxph(formula = formula, data = msdata, control = coxph.control(timefix = FALSE),
## model = TRUE, method = method)
##
## n= 26711, number of events= 11203
##
## coef exp(coef) se(coef) z Pr(>|z|)
## A1.1 -0.3277674 0.7205306 0.0289873 -11.307 < 2e-16 ***
## A1.2 0.1618408 1.1756730 0.0583132 2.775 0.00551 **
## A1.3 0.3003392 1.3503167 0.0614644 4.886 1.03e-06 ***
## A2.1 -0.2010490 0.8178723 0.0312703 -6.429 1.28e-10 ***
## A2.2 0.3346746 1.3974856 0.0604423 5.537 3.08e-08 ***
## A2.3 0.3314519 1.3929892 0.0681263 4.865 1.14e-06 ***
## c1.1 0.3899606 1.4769226 0.0249918 15.604 < 2e-16 ***
## c1.2 0.3874666 1.4732437 0.0464446 8.343 < 2e-16 ***
## c1.3 0.5001797 1.6490176 0.0397375 12.587 < 2e-16 ***
## c2.1 0.4906978 1.6334556 0.0134728 36.421 < 2e-16 ***
## c2.2 0.5040927 1.6554829 0.0237299 21.243 < 2e-16 ***
## c2.3 0.5753703 1.7777887 0.0224522 25.626 < 2e-16 ***
## M.3 -0.0004653 0.9995349 0.0088987 -0.052 0.95830
## A1.3:M.3 -0.1813485 0.8341446 0.0156937 -11.555 < 2e-16 ***
## A2.3:M.3 -0.2763646 0.7585364 0.0224230 -12.325 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## A1.1 0.7205 1.3879 0.6807 0.7627
## A1.2 1.1757 0.8506 1.0487 1.3180
## A1.3 1.3503 0.7406 1.1971 1.5232
## A2.1 0.8179 1.2227 0.7693 0.8696
## A2.2 1.3975 0.7156 1.2414 1.5732
## A2.3 1.3930 0.7179 1.2189 1.5920
## c1.1 1.4769 0.6771 1.4063 1.5511
## c1.2 1.4732 0.6788 1.3451 1.6136
## c1.3 1.6490 0.6064 1.5255 1.7826
## c2.1 1.6335 0.6122 1.5909 1.6772
## c2.2 1.6555 0.6041 1.5802 1.7343
## c2.3 1.7778 0.5625 1.7013 1.8578
## M.3 0.9995 1.0005 0.9823 1.0171
## A1.3:M.3 0.8341 1.1988 0.8089 0.8602
## A2.3:M.3 0.7585 1.3183 0.7259 0.7926
##
## Concordance= 0.652 (se = 0.003 )
## Likelihood ratio test= 3443 on 15 df, p=<2e-16
## Wald test = 3234 on 15 df, p=<2e-16
## Score (logrank) test = 3286 on 15 df, p=<2e-16
##
## # Relevant variable values:
## $a
## [1] "2"
##
## $astar
## [1] "0"
##
## $ref_table
## A M c1 c2
## 1 0 1 0 0
##
## $basecval
## c1 c2
## "0" "0"
##
## #Number of event in the data
## $Frequencies
## to
## from Start Mediator Outcome no event total entering
## Start 0 6711 1902 1387 10000
## Mediator 0 0 2590 4121 6711
## Outcome 0 0 0 4492 4492
##
## $Proportions
## to
## from Start Mediator Outcome no event
## Start 0.0000000 0.6711000 0.1902000 0.1387000
## Mediator 0.0000000 0.0000000 0.3859335 0.6140665
## Outcome 0.0000000 0.0000000 0.0000000 1.0000000
##
## #Point Estimation for time point of interest
## TE RD SD
## 1 0.03409689 0.02092829 0.0131686
## #SE for Point Estimation for time point of interest
## se_te se_rd se_sd
## 1 6.985263e-05 6.65853e-05 2.241292e-05
## #CI for Point Estimation for time point of interest
## TE RD SD
## 0.021939443 0.009187043 0.008910369
## TE RD SD
## 0.04697333 0.03343425 0.01718215
## #Point Estimation table for time point of interest
## TE RD SD
## Point estimate 0.0341 0.0209 0.0132
## 95% CI (0.0219, 0.047) (0.0092, 0.0334) (0.0089, 0.0172)
ggcmest(surv_catE)